In a previous article that I wrote, I showed that the classic evaluation of the so-called greenhouse effect (GHE) being in the order of 33K might be incorrect and that by the account of a few well known scientists, it could be smaller. But now, what if we are all mistaken?

What if there really were no GHE from CO2 at all?

Somebody who read my post, pointed me to a paper written in 2017 by Robert Ian Holmes. I show the abstract here:

Abstract: It has always been complicated mathematically, to calculate the average near surface atmospheric temperature on planetary bodies with a thick atmosphere. Usually, the Stefan Boltzmann (S-B) black body law is used to provide the effective temperature; then debate arises about the size or relevance of additional factors, including the ‘greenhouse effect’. Presented here is a simple and reliable method of accurately calculating the average near surface atmospheric temperature on planetary bodies which possess a surface atmospheric pressure of over 10kPa. This method requires a gas constant and the knowledge of only three gas parameters: the average near-surface atmospheric pressure, the average near surface atmospheric density and the average mean molar mass of the near-surface atmosphere. The formula used is the molar version of the ideal gas law. It is here demonstrated that the information contained in just these three gas parameters alone is an extremely accurate predictor of atmospheric temperatures on planets with atmospheres >10kPa. This indicates that all information on the effective plus the residual near-surface atmospheric temperature on planetary bodies with thick atmospheres, is automatically ‘baked-in’ to the three mentioned gas parameters. Given this, it is shown that no one gas has an anomalous effect on atmospheric temperatures that is significantly more than any other gas. In short; there can be no 33°C ‘greenhouse effect’ on Earth, or any significant ‘greenhouse effect’ on any other planetary body with an atmosphere of >10kPa. Instead, it is a postulate of this hypothesis that the residual temperature difference between the S-B effective temperature and the measured near-surface temperature is actually caused by adiabatic auto-compression.

Take the time to read the whole paper here:

https://sciencepublishinggroup.com/journal/paperinfo?journalid=161&doi=10.11648/j.earth.20170606.18

Holmes argues that the average temperature for 8 thick-atmosphere planetary bodies (0.1 bar or more) can be measured with high accuracy – an error range of only 1.2% – by using a formula based on the knowledge of 3 parameters: “[1] the average atmospheric pressure near the surface, [2] the average atmospheric density near the surface, and [3] the average molar mass of the nearby atmosphere.”

Holmes used the derived pressure/density/mass numbers for each planetary body. He then calculated the temperatures of the planets with these figures. The temperature of Venus was calculated to be 739.7 K with the formula. The measured temperature is 740 K. This indicates that the accuracy of the formula is within an error range of only 0.04% for Venus. Considering the pressure/density/mass of the Earth, the calculated temperature is 288.14 K using Holmes’ formula. The measured temperature on earth is 288 K, an exact fit. The calculated temperature of Saturn is 132.8 K. The measured temperature is 134 K – an error of only 0.89%. Apparently for Mercury, Mars and our moon the pressure would be too low to employ this method.

The impressive accuracy of the formula is shown in his Table 1 and in his Figure 2 of the paper (shown together here in one picture):

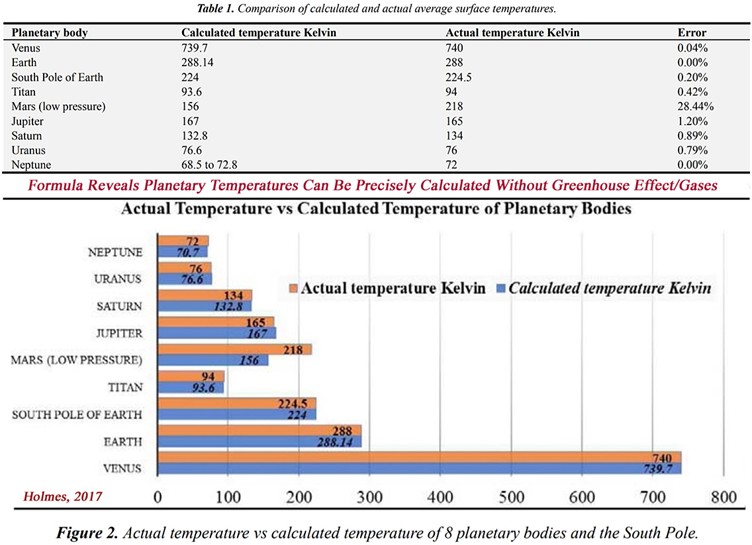
Discussion

After reading the whole report, the point that I think was the most convincing is the fact that Holmes calculated with an error of only 0.2% what the temperature at the South Pole is. Remember that most of the South Pole area lies at a height of almost 3000 meters above sea level, therefore the pressure and the air density differs considerably to that of earth between the -60 and +60 latitudes.  

Using Holmes’ formula, how much is the effect of more CO2 in the air, exactly?

It appears that the molar mass version of the Ideal Gas Law points to a very low climate sensitivity. I quote exactly what is says in the report, my own comment in brackets [ ] :

‘In particular, formula 5 (and 6) as presented here, totally rules out any possibility that a 33°C greenhouse effect of the type proposed by the IPCC in their reports [23] can exist in the real atmosphere. The reason is that the IPCC state in their reports that a 0.03% increase in atmospheric CO2 (i.e. a doubling from pre-industrial levels) must result in a global temperature rise of ca.3°C; (a range of 1.5°C to 4.5°C, which has hardly changed since 1990) [24]. This is the so-called ‘climate sensitivity’. Anything like this magnitude of warming caused by such a small change in gas levels is completely ruled out by the molar mass version of the ideal gas law.

Calculation for a doubling of CO2 from the pre-industrial level:

T = 101.33/ (8.314 x 1.226 /28.98)  [molecular weight of air changes only from 28.97 to 28.98 due to the doubling of CO2 from 0.03 to 0.06%]

Calculated temperature after doubling of CO2 from 0.03 to 0.06% ≈ 288.11K.  Climate sensitivity to CO2 is ≈ 288.14 – 288.11 ≈ – 0.03K. The change would in fact be extremely small and difficult to estimate exactly, but would be of the order -0.03°C. That is, a hundred times smaller than the ‘likely’ climate sensitivity of 3°C cited in the IPCC’s reports and probably be of the opposite sign [negative]. Even that small number would likely be a maximum change, since if fossil fuels are burned to create the emitted CO2, then atmospheric O2 will also be consumed, reducing that gas in the atmosphere – and offsetting any temperature change generated by the extra CO2. This climate sensitivity is already so low that it would be impossible to detect or measure in the real atmosphere, even before any allowance is made for the consumption of atmospheric O₂.

Holmes’ conclusion

‘There can be no significant ‘greenhouse warming’ caused by greenhouse gases on Earth, or for that matter on any other planetary body. Instead, it is proposed that the residual temperature difference on Earth, and the tropospheric thermal gradient observed, are actually caused by adiabatic auto-compression.’

[Holmes’ paper clearly defines auto compression – same formula is also used extensively in the mining industry to direct the flow of air – and he also explains the proposed adiabatic mechanism]